Coordinate Frames #

The previous discussion of motion profiling wraps up motion control for mechanisms with one degree of freedom. The remainder of the tour will extend these ideas to 2D robot movement.

Basics #

In order to describe 2D motion, we need a consistent global coordinate frame. Within this global frame, the robot’s position can be described using typical Cartesian \( (x,y) \) coordinates. In addition to the linear position, the robot has a heading \( \theta \) defined as the angle between the front of the robot and the global \( x \) axis. The position and heading together constitute the robot’s pose.

2D vectors and poses are built into the library and serve as primitives for many other classes.

Vector2d position = new Vector2d(x, y);
Pose2d pose = new Pose2d(position, theta);

val position = Vector2d(x, y)
val pose = Pose2d(position, theta)

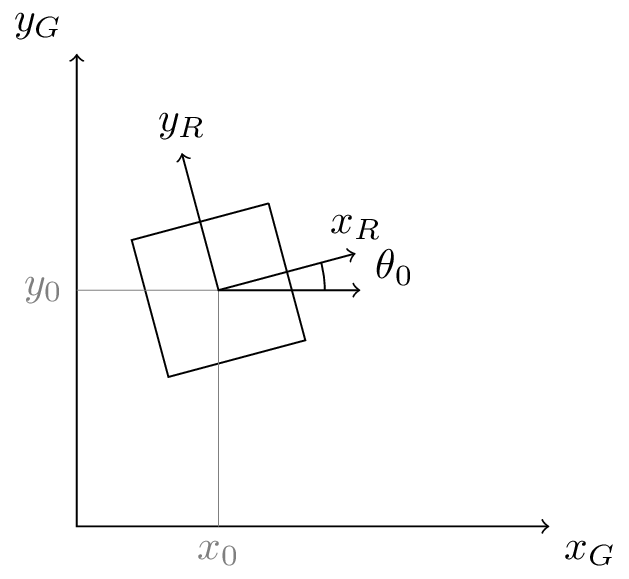
In addition to the global coordinate frame, there is a robot coordinate frame that moves along with the robot. Paths are more conveniently described in the global frame while robot velocities are more conveniently described in the robot frame. To accommodate this, Road Runner constantly switches between frames.

Transformations #

Consider a velocity vector \( \vec{v}_G \) in the global frame. To find the equivalent representation \( \vec{v}_R \) in the robot frame, we can apply a rotation transformation. This transformation can be represented by the following matrix:

If you haven’t seen matrices and vectors before, check out 3Blue1Brown’s series Essence of linear algebra. The first four videos are the most relevant to this section, although I strongly recommend all of them.

With this matrix, the transformation is simple: \( \vec{v}_G = R(\theta) \, \vec{v}_R \) . Since the inverse of \( R(\theta) \) is just \( R(-\theta) \) , \( \vec{v}_R = R(-\theta) \, \vec{v}_G \) . Note the angular velocity \( \omega \) remains the same between frames.

As you might expect, rotations are built into the Vector2d class:

Vector2d v = new Vector2d(x, y);
Vector2d w = v.rotated(rotAngleRad);

val v = Vector2d(x, y)
val w = v.rotated(rotAngleRad)

More sophisticated transformations can be found in Kinematics. For instance, the aforementioned pose-to-pose velocity transformation is Kinematics.fieldToRobotVelocity().